Resposta Problema 1 - Aplicações
| Para podermos resolver este problema precisaremos do desenho: |
 |
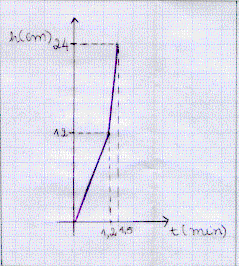
a) Vamos primeiro expressar o volume em função do tempo. Nós temos
que a vazão é constante, como a vazão é dada por: 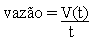 , temos que o volume aumenta proporcionalmente em relação ao
tempo, como a vazão é 1 l/min = 1 000 cm3/min, temos:
, temos que o volume aumenta proporcionalmente em relação ao
tempo, como a vazão é 1 l/min = 1 000 cm3/min, temos:
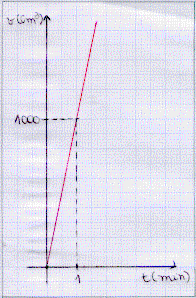
V(t) = 1000.t
| Com isso obtemos o gráfico ao lado: |
 |
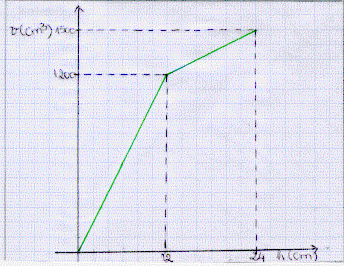
b) Agora, vamos achar o volume em função da altura. Para isso vamos
usar a fórmula do volume de um prisma de base quadrangular:
VOLUME = (ARESTA DA BASE)2 x ALTURA
Mas, vamos ter áreas da base diferentes para cada intervalo de tempo,
por isso, teremos 2 expressões para volume:
-
Para a parte maior do reservatório:
V(h) = a2.h para 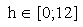
V(h) = 102.h = 100.h
- Para a parte menor do reservatório:
Devemos levar em conta que quando esta começar a encher teremos h = 12 cm
e V(h) = 100.12 = 1200 cm3, por isso a fórmula do volume será:
V(h) = a2(h - 12) + 1200 para 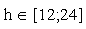
V(h) = 52.(h - 12) + 1200 = 25.(h - 12) + 1200
Com isso temos:
c) Finalmente, vamos descobrir a expressão da altura em função do
tempo. Para isso devemos novamente separar em dois casos. Mas, agora vamos
usar as fórmulas obtidas nos itens anteriores:
- Para a parte maior do reservatório, temos: V(t) = 1000.t e V(h) = 100.h,
por isso:
1000.t = 100 h(t)
h(t) = 10.t
Agora, só falta ver para qual intervalo de tempo vale esta expressão:
| altura mínima: | h = 0, t = 0; |
| altura máxima: | h = 12 cm
12 = 10.t
t = 1,2 min. |
- Para a parte menor do reservatório, temos:V(t) = 1000.t e V(h) =
25.(h - 12) + 1200, por isso:
1000.t = 25.(h(t) - 12) + 1200
1000.t = 25.h(t) - 300 + 1200
1000.t = 25.h(t) + 900
25.h = 1000.h(t) - 900
h(t) = 40.t - 36
De novo, só falta ver para que intervalo vale:
| altura mínima: | h = 12 cm
12 = 40.t - 36
40t = 48
t = 1,2 min
|
| altura mínima: | h = 24 cm
24 = 40.t - 36
40.t = 60
t = 1,5 min
|
Com isso, temos:
 Volta para Aplicações
Volta para Aplicações


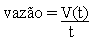 , temos que o volume aumenta proporcionalmente em relação ao
tempo, como a vazão é 1 l/min = 1 000 cm3/min, temos:
, temos que o volume aumenta proporcionalmente em relação ao
tempo, como a vazão é 1 l/min = 1 000 cm3/min, temos: 
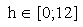
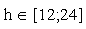
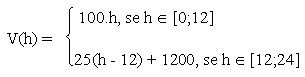
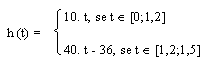
 Volta para Aplicações
Volta para Aplicações