Resposta Problema 2 - Aplicações

Para entender melhor o problema vamos fazer um desenho da situação:
Esta caixa que queremos contruir é na verdade um paralelogramo retângulo. Sabemos que a fórmula para calcular o volume de um paralelepípedo retângulo é:
VOLUME = ÁREA DA BASE x ALTURA = LADO1 X LADO2 X ALTURA
Como temos todos estes dados fica fácil calcular o volume da caixa:

V(x) = x.(1 - 2x).(1 - 2x)

Com o que temos já podemos fazer um esboço do gráfico do volume da caixa:

Para fazer o esboço do gráfico da função volume da caixa, primeiro verificamos quais são as raízes da função, vemos que as raízes da função são: 0 e 1/2(raiz dupla). Com isso sabemos que a função corta em x=0 e tangencia o eixo OX em x=1/2. Agora só falta vermos o que acontece entre as raízes e fora delas. Para x negativo V(x) é negativa, entre as raízes ela é positiva, e depois de x=1/2 também. Agora fica fácil traçar o gráfico ao lado: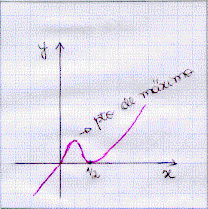

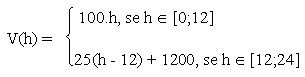
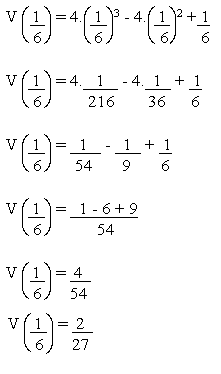
Com esse gráfico temos uma idéia de qual é o ponto de máximo, isto é, o maior volume que a caixa pode ter. Este ponto tem a primeira coordenada entre 0 e 0,5. Para saber com certeza qual será esse ponto devemos saber qual é a inclinação da reta tangente à curva.
V(x) = x.(1 - 4x + x2)
V(x) = 4x3 - 4x2 + x
Agora, vamos achar a derivada da função, que é o coeficiente angular da reta tangente. Vamos calculá-la para vermos quando ela é zero, pois assim a tangente será paralela ao eixo OX, vamos usar a generalização feita anteriormente:
V(x) = 4.x3 - 4.x2 + x


V '(x) = 3.4.x2 - 2.4.x + 1
V '(x) = 12.x2 - 8.x + 1

Agora podemos ver quando a inclinação da reta vale zero:
V '(x) = 12.x2 - 8.x + 1

Como já tínhamos visto que quando o volume é máximo, o valor da abcissa está entre 0 e 0,5, podemos concluir que o valor da primeira coordenada é 1/6. Agora só falta ver qual será o volume máximo, para isso substituímos o valor de x que encontramos na equação que nos dá o volume:

Volta para Aplicações