Resposta Problema 4 - Aplicações

Temos de construir uma lata cilíndrica com um litro de capacidade, usando o mínimo de material. Por isso deveremos minimizar a área total do cilindro. Antes devemos verificar quanto vale o volume do cilindro:VOLUME CILINDRO = ÁREA DO CÍRCULO x ALTURA, por outro lado temos que, VOLUME CILINDRO = 1 l = 1000 cm³. Igualando as duas expressões, obtemos:

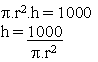
Agora, vamos ver qual é a expressão da Área do cilindro:

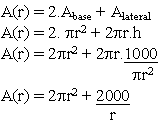
Já podemos fazer o esboço do gráfico área:

O gráfico da área é, na verdade, uma soma de outros dois gráficos, como sabemos fazer os "gráficos parcelas", fica fácil fazer o "gráfico soma".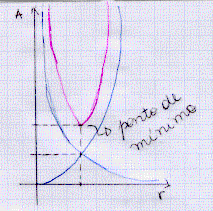

A partir do desenho, podemos ter uma idéia de qual é o ponto de mínimo dessa função. Mas, para podemos saber com certeza, através da função que nos dá a inclinação da reta tangente à curva, e verificarmos quando esta é igual a 0. Com o que temos, já podemos calcular a inclinação da reta tangente:

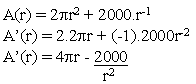
Agora, só falta vermos quando A'(x) = 0:

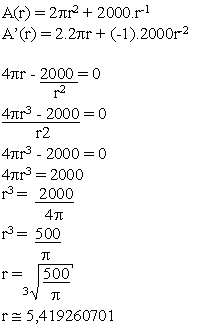
E o valor da altura será:

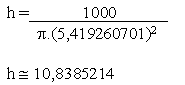
Observe que o valor encontrado para a altura é o dobro do valor do raio, isto quer dizer que para se utilizar o mínimo de material possível para a copnstrução de uma lata cilíndrica, devemos usar a relação: h = 2r.

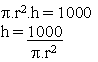
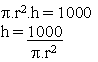
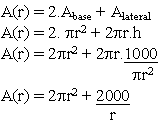
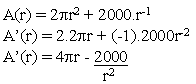
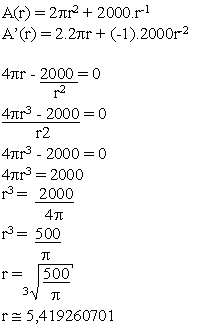
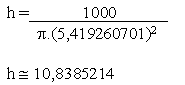
Volta para Aplicações