Resposta Problema 5 - Aplicações
Neste problema devemos maximizar a área para banho, tendo 160 m de corda
para delimitar esta região retangular. Então, vamos ver como fica o
perímetro:
P = 2x + 2y
160 = 2(x + y)
x + y = 80
y = 80 - x
Agora, vamos ver a expressão da área da região retangular:
A = x.y
A(x) = x(80 - x)
A (x) = 80x - x2
Podemos fazer o esboço do gráfico área:
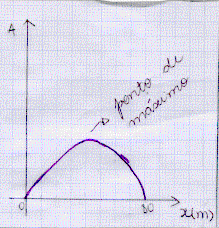
No gráfico podemos visualizar o ponto de máximo dessa função, podemos
perceber que a primeira coordenada está entre 0 e 80. Para determinarmos o
ponto de máximo devermos verificar quando a inmclinação da reta tangente à
curva é igual a 0. Para isso vamos calcular qual é a função que nos fornece a
inclinação da reta tangente à curva (área):
A'(x) = 80 - 2x
Só falta ver quando A'(x) = 0:
80 - 2x = 0
2x = 80
x = 40 m
E verificar qual o valor de y:
y = 80 - x
y = 80 - 40
y = 40 m
Volta para Aplicações