ATIVIDADE I

No programa CABRI GEOMETRY, siga os passos abaixo:

• Marque três pontos quaisquer (Menu 2/Item 1)
• Construa duas semi-retas com origem no mesmo ponto (Menu 3/Item 3)
• Meça o ângulo formado por essas duas semi-retas (Menu 9/Item 4)

• Movimente os pontos P e Q e veja o que acontece com o valor da medida do ângulo.
  

  ATIVIDADE II
  

  Vamos descobrir, nesta Atividade, algumas relações entre ângulos e retas paralelas.
  
  • Construa as três retas abaixo (Menu 3/Item 1), usando para isso 6 pontos, e marque os ângulos formados por elas (Menu 10/Item 4).
  
  
  • Movimente as retas e observe o que acontece com os ângulos marcados. Em qual posição das retas conseguimos um maior número de ângulos iguais?
  • Coloque-as na posição abaixo e meça seus ângulos.
  • O que você percebeu?
  Resposta
  
  
  

  ATIVIDADE III
  

  Nesta Atividade, vamos medir os ângulos internos de um triângulo qualquer e calcular sua soma.

  
  Exercício 1
  • Construa um triângulo qualquer (Menu 3/Item 5) e meça seus ângulos internos.
  • Vá ao Menu 9/Item 6 (Calculate) para ativar a calculadora e some os três ângulos internos do triângulo que você construiu. Para fazer isto, certifique-se de que o cursor está na janela da calculadora, aproxime o mouse do número desejado e clique. Em seguida, clique em + e siga o processo.
    Para que o resultado permaneça na tela após fecharmos a calculadora, aproxime o mouse do resultado e arraste-o para a tela.
  
  
  
  
  • Movimente os vétices do triângulo. O que acontece com a soma de seus ângulos?
  
  
  Exercício 2

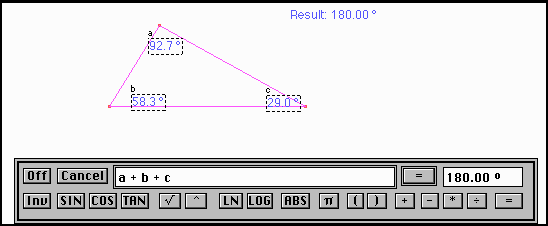
  Refaça a construção abaixo, seguindo os passos indicados:

  
  
  Você precisará aplicar um movimento de reflexão aos triângulos verde, laranja e azul em torno das retas indicadas na figura (as retas verticais são perpendiculares à reta suporte do lado do triângulo). Para isso, utilize o Menu 6/Item 4.

  Movimente os vértices do triângulo e veja o que acontece.

  O que podemos perceber com este exercício?

  Como fica o caso em que o ângulo laranja ou o azul é obtuso?

  
  Exercício 3

  As retas pontilhadas da figura abaixo são paralelas. Observe os ângulos do triângulo.

  

  Movimente os vértices do triângulo e veja o que acontece com a figura.

  De que podemos nos convecer depois de realizar estes três exercícios?
  Resposta

  
  

  ATIVIDADE IV
  

  Vamos estudar os ângulos nos quadriláteros.

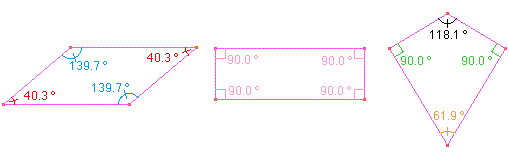
  Construa um polígono qualquer de quatro lados. Existe alguma relação entre os ângulos desse polígono?

  

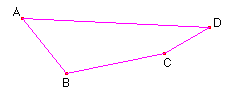
  Movimente seus vétices. Que figuras podemos obter? Como são os ângulos dessa figura? Em que situação os ângulos opostos dessa figura têm mesma medida?
  Resposta

  Construa as figuras abaixo, que guardam propriedades em relação aos ângulos, sob a ação do movimento.

  
  
  

  ATIVIDADE V
  

  Nesta Atividade, vamos entender o conceito de Rotação.

  Para rotacionarmos uma figura qualquer, precisamos de um ponto O para centro de rotação e um ângulo a para ângulo de rotação. Observe a figura ao lado. A baideira "gira" em torno do ponto O, um ângulo a.

  O movimento de rotação é uma transformação isométrica do plano, ou seja, não "deforma" a figura inicial.

  Para rotacionar uma figura no CABRI, basta utilizar o Menu 6/Item 2 e indicar com mouse a figura que queremos rotacionar, o centro e o ângulo de rotação. Lembre-se que o CABRI rotaciona a figura no sentido anti-horário. Explore este menu.

  
  

  ATIVIDADE VI
  

  Utilizando o princípio de rotação e alguns polígonos regulares, vamos construir mosaicos.

  1. Mosaicos a partir de Quadrados

  Descubra o centro e o ângulo de rotação necessários para construir, no CABRI, o mosaico ao lado, a partir de um quadrado.

  2. Mosaicos a partir de Triângulos Equiláteros

  Descubra o centro e o ângulo de rotação necessários para construir, no CABRI, o mosaico ao lado, a partir de um triângulo equilátero.

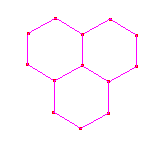
  3. Mosaicos a partir de Hexágonos

  Descubra o centro e o ângulo de rotação necessários para construir, no CABRI, o mosaico ao lado, a partir de um hexágono.

  Resposta

  
  DESAFIO: Você é capaz de construir mosaicos com outros polígonos regulares, de maneira que o encaixe fique perfeito, utilizando ângulo de rotação inteiro?
  Resposta
  
  
  
  PROJETO:
  MECANISMOS COM PRINCÍPIO DE ROTAÇÃO

  Os mecanismos abaixo foram construídos com o princípio de rotação. Observe-os e tente construir seus próprios mecanismos.

  Roda Gigante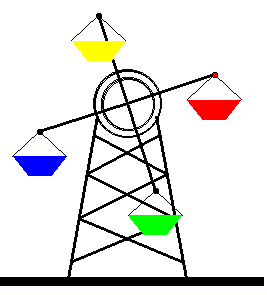
  
  
  
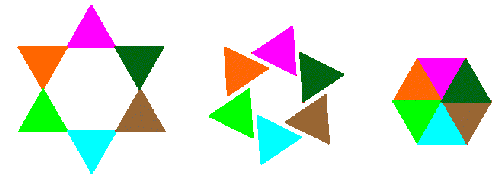
  Estrela/Hexágono
  
  
  

  Veja essas construções em Animação Java!