
ATIVIDADE I
Nesta atividade, vamos aprender a utilizar dois Macros que nos serão necessários nas atividades seguintes: copiaseg.mac e copiang.mac. Estes Macros, disponíveis na pasta macros do Cabri, copiam segmentos e ângulos. Vamos entendê-los:
| copiaseg.mac: Este macro copia um segmento qualquer para uma semi-reta. Para utilizá-lo, precisamos indicar o segmento que queremos copiar e a semi-reta na qual queremos "colocar a cópia". |
 |
| copiang.mac: Este macro copia um ângulo qualquer, definido por 3 pontos, colocando um dos lados sobre uma semi-reta. Para utilizá-lo, precisamos indicar os 3 pontos que definem o ângulo e a semi-reta na qual queremos "colocar um dos lados do ângulo". |
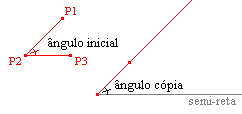 |
ATENÇÃO: Exercite estes macros no CABRI para uma maior familiarização.
ATIVIDADE II
Dois triângulos são congruentes quando conseguimos sobrepor um ao outro, fazendo com que eles coincidam.
Construa um triângulo congruente ao triângulo abaixo da maneira que achar mais fácil, matendo a estabilidade das figuras de tal forma que quando "deformarmos" o primeiro, o outro deve "deformar-se" também, mas mantendo a congruência.
Veja a solução na atividade seguinte.
ATIVIDADE III
Caso 1: LAL - Lado/Ângulo/Lado
Construa um triângulo,dados dois lados e o ângulo formado entre eles.

Quantos triângulos você consegue construir com estes três elementos?
Resposta
Caso 2: LLL - Lado/Lado/Lado
Construa um triângulo,dados seus três lados.
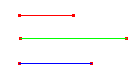
Quantos triângulos você consegue construir com estes três elementos?
Resposta
Caso 3: ALA - Ângulo/Lado/Ângulo
Construa um triângulo,dados dois ângulos e o lado compreendido entre eles.
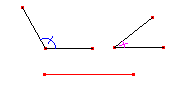
Quantos triângulos você consegue construir com estes três elementos?
Resposta
ATIVIDADE IV
Nesta atividade, vamos estudar os Pontos Notáveis de um Triângulo.
Mediatriz: Mediatriz de um segmento é a reta perpendicular ao segmento que passa pelo seu ponto médio.
Construa um triângulo e duas de suas mediatrizes. A seguir, construa um círculo com
centro no ponto de encontro das duas mediatrizes e que passe por um dos vértices do
triângulo. Movimente os vértices desse triângulo. O que você observa? Construa a terceira
mediatriz. O que você conclui?
Resposta
Bissetriz: Bissetriz de um ângulo é a semi-reta que divide este ângulo em dois ângulos de mesma medida.
Construa um triângulo e duas de suas bissetrizes. A seguir, construa um círculo com
centro no ponto de encontro das duas bissetrizes e que tangencie seus lados. Movimente os
vértices do triângulo; o círculo deve permanecer tangente.
Resposta
Altura: Altura de um triângulo é o segmento que vai, perpendicularmente, de um dos vértice do triângulo à reta suporte do lado oposto a este vértice.
|
Construa um triângulo. Trace as retas suporte de suas três alturas. A seguir, construa
um segundo triângulo de tal forma que seus lados sejam paralelos aos lados do primeiro e
passem pelos três vértices. Movimente os vértices do primeiro triângulo e descubra qual a
relação entre a reta suporte das alturas com o triângulo maior? |
 |
ATIVIDADE V
Esta é uma atividade básica, onde perceberemos os movimentos
de translação, rotação e reflexão. Movimento de Translação Movimento de Rotação Movimento de Reflexão
Exercício 2:
Exercício 2:
Exercício 2:
Vamos aprender a construir mosaicos cujos pricípios de construção são as transformações isométricas. Inicie brincando com os mosaicos abaixo.
Mosaico 1
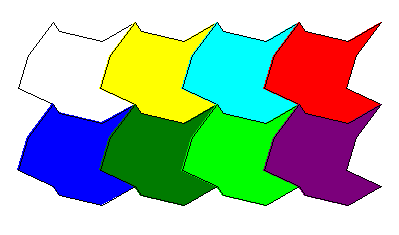
Mosaico 2
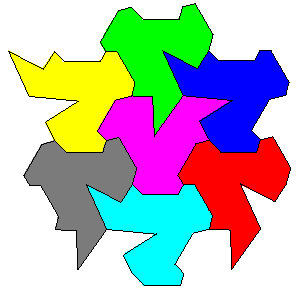
Procure descobrir o princípio de construção destes mosaicos.
Ajuda
Vamos montar alguns quebra-cabeças. Queremos, a partir de uma figura, montar outra. Por exemplo: transformar um triângulo equilátero em um retângulo; transformar um retângulo em um quadrado; transformar um polígono qualquer em um retângulo, etc.
A seguir, temos algumas figuras que foram divididas com critérios muito particulares. Procure descobrir os critérios utilizados e em seguida monte um quadrado com cada uma dessas figuras.
PRIMEIRA FIGURA
 |  |
 |
SEGUNDA FIGURA
 |
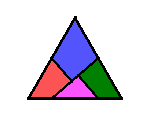 |  |
TERCEIRA FIGURA
 |
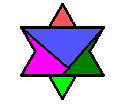 |  |
QUARTA FIGURA
 |
 |  |