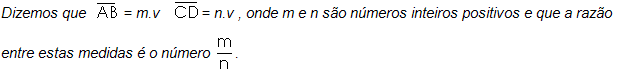NÚMEROS REAIS E MEDIDAS
Recapitulando
Nos módulos anteriores, construímos dois conjuntos numéricos:
1)Conjunto dos inteiros {0,1,2,3...}
No módulo II, a construção dos racionais foi feita
na perspectiva da aritmética das operações com números
inteiros. As frações foram definidas como quocientes de
inteiros, que não são necessariamente inteiros.
Esta construção pode ser feita, também,
numa perspectiva geométrica, a partir do conceito de medida de
segmentos.
O Problema da medida – Construção do Campo Racional
O processo de medida consiste em comparar um segmento arbitrário
com outro fixado como unidade.
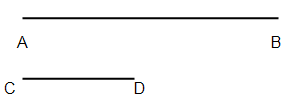
Aplicamos um sobre o outro, fazendo coincidir dois extremos A e C.
Vemos que o ponto D cai entre A e B e expressamos o resultado da comparação:
Mas não basta informar que um comprimento é “maior
que” o outro. Às vezes necessitamos saber quantas vezes cabe
um comprimento no outro.
Para isto é necessário um termo de comparação
para todas as grandezas de uma mesma espécie, ao qual denominamos
de “unidade de medida”.
1) É necessário estabelecer um termo único de comparação
para todas as grandezas da mesma espécie, a este termo chamamos
unidade de medida. No caso da medida de segmentos, a unidade pode ser
centímetros, metros, pés, jardas, etc.
2) É necessário responder à pergunta: Quantas vezes?
A resposta consiste em achar um número que expresse o resultado
da comparação com a unidade. Este número é
a “medida da grandeza em relação a essa unidade”.
|
|
Escolhemos v como unidade de medida e temos as seguintes igualdades:
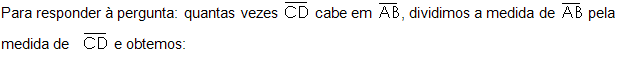
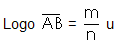
Define-se o número m/n como a razão entre as medidas dos
dois segmentos.
|
|
|
Definição |
A crise da medida: a definição de irracional
Por muito tempo se pensou que dois segmentos quaisquer
eram sempre comensuráveis.
A ilusão da comensurabilidade durou até o quarto século
antes de Cristo. Naquela época, em Crotona, sul da Itália,
havia uma seita filosófico-religiosa, liderada por Pitágoras.
Um dos pontos fundamentais de sua doutrina era o lema "Os números
governam o mundo", sendo que, para eles, números eram números
naturais sobre os quais se podia estabelecer relações, tomar
razões e, conseqüentemente, formar frações.
Estudando geometria, Pitágoras conseguiu demonstrar
que, para qualquer triângulo retângulo, o quadrado da hipotenusa
é igual a soma dos quadrados dos dois catetos (Veja
a visualização do Teorema Pitágoras).
A partir deste resultado, surgiu um número que corresponde à
razão entre as medidas da
medida da diagonal do quadrado de lado 1.
Na época, a crença na comensurabilidade de qualquer par
de segmentos, fez pensar que o 
Porém, buscando a razão entre estes segmentos, um dos discípulos
de Pitágoras, observou que eles não são comensuráveis.
Não existe um segmento-padrão, unitário, que cabe
um 
(Veja
a Demonstração da incomensurabilidade da diagonal e do lado
do quadrado).
Este foi um momento de ruptura e de crise, entre os estudiosos da época.
Aparecia pela primeira vez na história da Matemática, a
possibilidade da existência de segmentos incomensuráveis
e, conseqüentemente, segmentos cuja razão entre as medidas
não resulta em números racionais. Abria-se a possibilidade
da existência de outro tipo de números: os números
irracionais.
|
A existência de segmentos incomensuráveis
implica na insuficiência dos sistemas numéricos conhecidos
– números naturais e racionais - para efetuar medidas
dos objetos geométricos mais simples, como o quadrado e
o círculo. |
|
Definição Um número irracional é um
número que representa a medida de um segmento incomensurável
com a unidade. |
Com esta definição, podem-se encontrar
muitos exemplos de irracionais.
Aplicando o Teorema
de Pitágoras¹,
verifica-se que a diagonal do quadrado de lado unitário é
o número 
.
Demonstra-se que 
é
irracional, assim como todas as raízes não
exatas de números naturais são irracionais.
Outro número importante na história
grega, que também é irracional, é o Número
de Ouro, o número da beleza e da harmonia, também representado
por radicais.
Foi demonstrado (com mais dificuldade) que o número
que
corresponde à medida do comprimento da circunferência de
diâmetro unitário, é irracional, mas não pode
ser representado por um radical, ou seja nem todos os irracionais são
raízes de inteiros.
O conjunto dos irracionais é resultado da união de dois
conjuntos: o conjunto dos irracionais algébricos (representados
por radicais) e o conjunto dos irracionais transcendentes (número
que não se apresentam na forma de radicais). Não vamos demonstrar,
neste estudo, mas existe um resultado interessantíssimo sobre estes
conjuntos: existem mais números transcendentes do que números
algébricos² .
A semi-reta é uma metáfora para os números
reais não negativos.
Pode-se construir uma semi-reta numerada, dotando-a de uma origem O, determinando
um sentido para efetuar medidas, e escolhendo alguma unidade de medida
para marcar pontos correspondentes aos números inteiros, à
direita de O. Deste modo, cada ponto P da reta é identificado com
a extremidade de um segmento OP e associado ao número que corresponde
à medida deste segmento. O zero corresponde a um segmento nulo,
obtido quando P coincide com O.
| Definição O conjunto dos números reais (positivos)
é definido como o conjunto de todos os números que
correspondem a medidas de segmentos não nulos, da reta.
|
| Diagrama
|
Conclusões
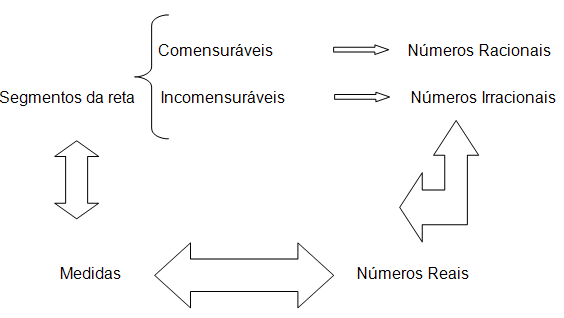
O conjunto dos números reais resulta da união de dois conjuntos
numéricos: o conjunto dos números racionais e dos números
irracionais.
O conjunto dos números reais é o conjunto dos números
que representam medidas de segmentos da reta. O conjunto dos números
racionais corresponde à medida de segmentos comensuráveis
com a unidade e o dos irracionais corresponde à medida de segmentos
incomensuráveis com a unidade.
Por definição, a cada ponto da (semi)reta real corresponde
um segmento, cuja medida é um número real e reciprocamente
a cada número real corresponde um segmento representado por um
ponto da reta.
Convém lembrar que demorou muito tempo para se aceitar e se incorporar
aos conjuntos numéricos os números negativos e o 0. Incorporando-os,
finalmente é definida a reta real.
A
reta real completa é dividida em duas semi-retas
e, por convenção, a semi-reta à direita do zero é
o lugar dos números positivos; a semi-reta à esquerda é
construída por simetria e contém números negativos,
definidos como os opostos dos positivos. Estes números passaram
a ser identificados por sinais: à direita, números positivos,
(+x) e à esquerda, números negativos, identificados com
o sinal (-x). Estes números foram definidos como sendo os opostos
aditivos, também denominados de simétricos, dos reais positivos:
(+x) + (-x) = x – x = 0.
Ao compararmos a reta completa com a semi-reta inicial, cujos números
não são assinalados (não têm sinal), passamos
a identificar os números com sinal + com os números conhecidos.
sinal de +, basta apresentá-los, sem sinal, como usualmente se
apresenta uma medida.
Considerando a reta completa e o conjunto dos reais também completo,
com a incorporação dos negativos, afirma-se que o conjunto
dos números reais é equivalente ao conjunto dos pontos da
reta, isto é, existe uma correspondência biunívoca:
a cada ponto um número e a cada número um ponto.
Axioma da completude
Com esta relação entre a reta e o conjunto
dos reais, fica implícita a noção da continuidade
(ou completude), deste conjunto. Intuitivamente, o conjunto dos números
reais é contínuo ou completo como a reta.
No entanto, o conceito de continuidade ou de completude é
dos mais difíceis e abstratos da Matemática³
.
_____________________________________________________________________________
¹Se você
quiser ver outra demonstração do Teorema de Pitágoras,
assista:
http://www.youtube.com/watch?v=lRqVfuEPdN4
http://www.youtube.com/watch?v=dUbVnb2LDLU&feature=related
²Se
você quiser saber mais sobre o assunto:
http://www.dmm.im.ufrj.br/~risk/diversos/tamanho.html
http://euler.dmat.ufpe.br/gradua/intervalo/ciencia_horje_infinito.pdf
³Se você
quiser saber mais sobre o assunto:
www.sbempaulista.org.br/epem/anais/co.html
ou Texto:
Lógico e histórico.
_____________________________________________________________________________
GLOSSÁRIO
Correspondência
biunívoca
Medida
Numero
irracional
Numero
irracional algébrico
Numero
irracional transcendente
Número
real
Segmentos
comensuráveis
Segmentos incomensuráveis
BIBLIOGRAFIA
CARAÇA, Bento de Jesus. Conceitos Fundamentais de Matemática.
Lisboa: Gradiva, 1998.
CERRI, Cristina. Desvendando
os Números Reais (pdf). IME-USP. Novembro de 2006. Disponível
em http://www.mat.ufg.br/bienal/2006/mini/cristina.cerri.pdf
DIAS, Marisa.; COBIANCHI, Antonio Sérgio. Correlação
do lógico e do histórico no ensino dos números reais
(pdf). In: VII Encontro Paulista de Educação Matemática,
2004, São Paulo. Disponível em:. www.sbempaulista.org.br/epem/anais/co.html
FRID, Hermano. Os
números irracionais (pdf). Revista Eureka. Disponível
em www.obm.org.br/eureka/artigos/irracionais.doc
LIMA, Elon Lages, CARVALHO, Paulo César pinto, WAGNER, Eduardo,
MORGADO, Augusto César. A Matemática do Ensino Médio.
Coleção do Professor de Matemática. Vol. 1. Sociedade
Brasileira de Matemática, 2001.
