
LOGARITMOS
1. INTRODUÇÃO HISTÓRICA
No fim do século XVI, o desenvolvimento da Astronomia e da Navegação exigia longos e laboriosos cálculos aritméticos, que nos anos próximos de 1600, era um problema fundamental. Procurava-se então um processo que permitisse reduzir cada operação de multiplicação, divisão, potenciação e radiciação em adição e subtração.
Esta descoberta científica foi feita simultaneamente por duas pessoas trabalhando independentemente. Não se trata de simples coincidência: tal descoberta corresponde à solução de um problema importante, do qual muitos se vinham ocupando.
Os logaritmos foram descobertos por. Jost Bürgi (1552-1632), suíço, relojoeiro, matemático e inventor, e Jhon Napier (1550 – 1617), um nobre escocês, teólogo e matemático, cada um deles desconhecendo inteiramente o outro, publicaram as primeiras tábuas de logaritmos. As tábuas de Napier foram publicadas em 1614 e as de Bürgi em 1620.
Uma tábua de logaritmos consiste essencialmente de duas colunas de números. A cada número da coluna à esquerda corresponde um número à sua direita, chamado o seu logaritmo. Para multiplicar dois números, basta somar seus logaritmos; o resultado é o logaritmo do produto. Para achar o produto, basta ler na tábua, da direita para a esquerda, qual o número que tem aquele logaritmo. Semelhantemente, para dividir dois números basta subtrair os logaritmos. Para elevar um número a sua potência basta multiplicar o logaritmo do número pelo expoente. Finalmente, para extrair a raiz n-ésima de um número, basta dividir o logaritmo do número pelo índice da raiz.
Logo depois do aparecimento da primeira tábua de logaritmos de Napier, o matemático inglês Henry Briggs (1561 – 1631), professor da Universidade de Londres, e depois de Oxford, elaborou, juntamente com Napier, uma nova tábua. Utilizou os chamados logaritmos decimais, ou logaritmos ordinários, que tiram proveito do fato de usarmos um sistema de numeração decimal.
Durante os trezentos e cinqüenta anos sucederam à descobertas dos logaritmos, sua utilidade revelou-se decisiva na Ciência e na Tecnologia. Já Kepler, por volta de 1620, atestava seu reconhecimento pela nova descoberta que segundo ele “aumentava vastamente o poder computacional do astrônomo”. O próprio Napier, um tanto imodestamente, reconhecendo o valor de sua descoberta, deu às suas tábuas o título Mirifici logarithmorum cononis descriptio, que significa Uma descrição da maravilhosa regra dos logaritmos.
Recentemente, com a utilização cada vez mais divulgada dos computadores, as tábuas de logaritmos perderam algo do seu poder como instrumento de cálculo, o mesmo acontecendo com as outras tabelas de matemáticas. Mas há diversas razões pelas quais o estudo de logaritmos ainda é o continuará a ser de central importância.
A principal dessas razoes é de natureza teórica. Embora eles tenham sido inventados como acessório para facilitar operações aritméticas, o desenvolvimento da matemática e das ciências em geral veio mostrar que diversas leis matemáticas e vários fenômenos naturais e mesmo sociais são estreitamente relacionados com os logaritmos. Assim sendo, os logaritmos, que no princípio eram importantes apenas por causa das tábuas, mostraram ter apreciável valor intrínseco.
2. DEFINIÇÃO
Chamamos de logaritmo de a, na base b, ao número c, tal que:
![]()
Onde:
a = logaritmando
b = base
c = logaritmo
Uma observação importante sobre o estudo dos logaritmos
diz respeito ao seu domínio ou campo de existência. Só
existem logaritmos de números positivos, com bases também
positivas e diferentes de 1. Ou seja, para calcular o logaritmo de a,
na base b, é necessário que a > 0, b>0 e b?1.
Desta forma, podemos afirmar que:
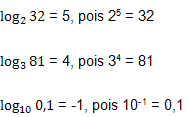
2.1 ALGUNS LOGARITMOS ESPECIAIS:
1) O logaritmo da unidade, em qualquer base, é nulo, ou seja:
![]()
2) O logaritmo de um valor, na mesma base, é sempre igual a 1,
ou seja:
![]()
3) O logaritmo de uma potência, cuja base seja igual à base
do logaritmo, será igual ao expoente da potência.
![]()
4) Se log M = log N então podemos concluir que M = N.
Esta propriedade é muito utilizada na solução de
exercícios envolvendo equações onde aparecem logaritmos
(equações logarítmicas).
5) b elevado ao logaritmo de M na base b é igual a M
![]()
3. BASES ESPECIAIS
Entre as bases de logaritmos, duas se destacam, tanto pela sua aplicabilidade
prática, quanto pela sua importância no trato com logaritmos.
Estas duas bases são a base dez e a base e.
3.1. BASE DEZ:
Quando um logaritmo apresenta a base dez, dizemos que se trata de um logaritmo
decimal. A base dez, por convenção, não precisa ser
escrita. Veja os exemplos:
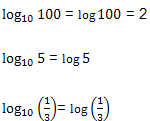
3.2. BASE e:
O número e, é conhecido como número de Euller e vale
aproximadamente 2,718... Este número tem origem na expressão:
![]()
Quando um logaritmo possui base e, ele é chamado
de logaritmo neperiano, e representado por ln. Deste modo:
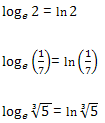
4. MUDANÇA DE BASE
A base de um logaritmo pode ser modificada de acordo com a necessidade
ou com os dados de um determinado problema. Um bom exemplo de necessidade
de mudança de base de logaritmos é a utilização
das calculadoras. Como vimos anteriormente, as calculadoras trabalham
apenas com a base 10 e base e. Desta forma, se quisermos encontrar, utilizando
calculadoras, o valor de um logaritmo que não esteja numa destas
duas bases, precisamos modificá-la.
Para mudar a base de um logaritmo utilizamos a seguinte relação:
![]()
Deste modo, podemos estabelecer as seguintes igualdades:
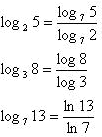
5. PROPRIEDADES DOS LOGARITMOS
Foi dito, no início deste texto, que os logaritmos permitem transformar
multiplicações em somas e subtrações em divisões,
entre outras alterações que visam facilitar o trato dos
números.
Estas transformações são possíveis com a utilização
das propriedades dos logaritmos, que veremos a seguir.
5.1 LOGARITMO DO PRODUTO:
![]()
5.2 LOGARITMO DO QUOCIENTE:
![]()
5.3 LOGARITMO DA POTÊNCIA:
![]()
5.3.1 CASO PARTICULAR: LOGARITMO DE RAIZ:
Um caso particular da propriedade de logaritmo da potência, é
o logaritmo de raízes. Para tanto, basta transformar a raiz nma
potência de expoente fracionário, conforme o modelo a seguir:
![]()
6. FUNÇÃO LOGARITMICA
6.1 DEFINIÇÃO
Chamamos de função logarítmica, à função
da forma
![]()
6.2 DOMÍNIO E IMAGEM
Percebe-se, da definição de logarítmos, que esta
fnção deve apresentar os seguintes conjuntos para domínio
e imagem:
![]()
Imagem: Reais
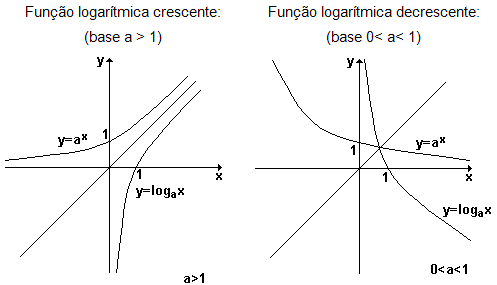
6.3 GRÁFICOS DE FUNÇÕES LOGARITMICAS
Observe os gráficos das funções logarítmicas
a seguir, que estão comparados aos gráficos das suas respectivas
funções inversas. Lembre-se que o gráfico de uma
função e o da sua inversa são simétricos em
relação á bissetriz dos quadrantes ímpares
(reta x = y).
7. APLICAÇÔES


Sem dúvida é um número gigantesco. Agora observe
que:
log 3 = 0,477121
log 20 = 1,301030
log 570 = 2,755875
log 6780 = 3,831230
log 10990 = 4,040998
log 325400 = 5,512418
Percebeste o que está acontecendo?
A parte inteira do logaritmo chama-se característica
e a parte decimal chama-se mantissa.
Por exemplo, log 570 =2,755875. A característica é 2
(parte inteira) e a mantissa é 0,755875.
Agora observe que se você determina o logaritmo de um número
que tem 5 algarismos, a resposta obtida começará pelo número
4. Se você determina o logaritmo de um número de 3 algarismos,
a resposta obtida começará pelo número 2. Ou seja,
a característica será sempre a quantidade de algarismos
do número menos um.

Segue que log x = 1000 log 2.
Daí log x = 1000 . 0,301029995.
Finalmente log x = 301,0299957.
Se a característica é 301 significa que x tem 302 algarismos,
ou seja, não se sabe ![]()