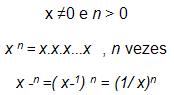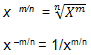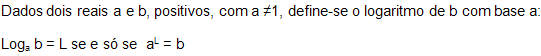RADICIAÇÃO, POTENCIAÇÃO, LOGARITMAÇÃO
Potência
POTENCIAÇÃO, RADICIAÇÃO E LOGARITMAÇÂO NOS NÚMEROS REAIS
Potenciação¹
Neste texto, ao classificarmos diferentes casos de potenciação,
vamos sempre supor ![]() indeterminação.
indeterminação.
Caso 1: Expoente inteiro n positivo e (-n) negativo
|
Condições: x real e n inteiro
|
Todas as propriedades que já foram demonstradas para bases inteiras
ou racionais continuam válidas.
Justificativa
![]()
Exemplos:
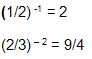
Radiciação
|
Condições: x real e n inteiro |
Caso 2: Expoente racional m/n positivo ou negativo
| Condições: x real e m/n racional
|
As propriedades já demonstradas continuam válidas e são estendidas para números reais.
Exemplos:
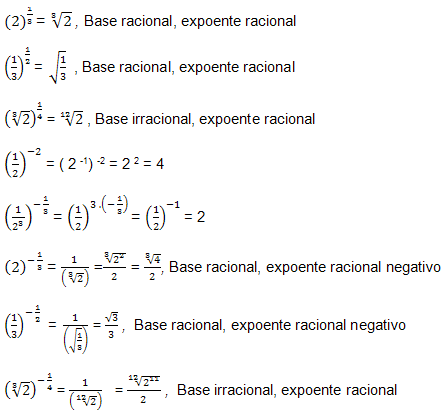
Observamos que, neste caso, as potências com base
racional e expoente racional produzem números irracionais.
Caso 3: Expoente real qualquer.
|
Condições: x real e y real |
Estamos interessados em definir potências cujo
expoente é irracional, como por exemplo ![]()
![]() 1,4; 1,41; 1,414; 1,4142; .....
1,4; 1,41; 1,414; 1,4142; .....

Este número é irracional e só pode ser expresso como
uma aproximação por racionais.
![]()
1,41 = 141/100 = 1 + 41/100
![]()
É um número irracional, real, positivo e só podemos
ter uma aproximação decimal, 
Sabemos que você não conhece a definição formal
de “limite de seqüências”.
Neste momento do curso, queremos apenas que você aceite a idéia
de que todas as operações sobre irracionais podem ser efetuadas,
mas são efetuadas por aproximação porque estamos
usando seqüências de racionais que se aproximam do número.
O número de casas decimais utilizadas no número irracional
significa que estamos selecionando elementos mais ou menos próximos,
da seqüência que se acumula sobre nosso irracional.
Exemplos:
![]()
Neste tipo de cálculo, usamos a calculadora e
aproximações decimais. Nestes exemplos, 2 ou 3 casas depois
da vírgula.
Caso 4: Base real negativa
É preciso investigar o caso das potências
com base real negativa.
Já vimos que para bases positivas, racionais ou reais, a potência
pode sempre ser definida, para qualquer expoente real não nulo.
O que ocorre com a base negativa?
Não há problemas, se o expoente for inteiro:
(-2)³ = (-2)(-2)(-2).
![]()
(todo real elevado ao quadrado resulta em número positivo e (-4)
é negativo).
![]()
Mas há um problema, que surge da equivalência de frações.
Sabemos que
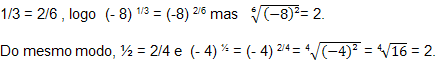
|
Ou seja, uma potência com expoente racional
de um número negativo não pode ser definida. |
Contra-exemplos:

Operações com Radicais
As operações com radicais ficam mais claras, quando os representamos
por potências:
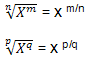
Multiplicação
1. Radicais com mesma base e expoentes diferentes. Transformam-se em potências
de mesma base. Mantém a base e soma os expoentes:
![]()
Exemplo :
![]()
Vale para a divisão
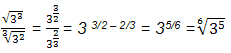
2. Radicais com mesmo expoente e bases diferentes. Transformam-se em potências
de mesmo expoente. Multiplica as bases e mantém o expoente.
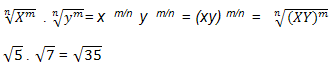
Vale para divisão
![]()
Veja o exemplo para bases iguais e expoentes também iguais:
![]()
Ou
![]()
Adição e subtração
É impossível aplicar regra semelhante na adição
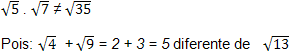
Só é possível adicionar e subtrair radicais com bases
iguais e expoentes iguais.
![]()
Logaritimação²
|
|
Exemplos:

Como a definição exige que a base seja
positiva, não existe número real correspondente a logaritmo
negativo.
Procure o Texto
Logaritmos e estude mais sobre o assunto.
Conseqüência deste estudo, percebe-se a insuficiência
do campo dos reais para dar significado a diferentes símbolos:
| Existem simbolos formados com números reais, utilizando as operações de potenciação, radiciação e logaritmação que não correspondem a números reais. |
Os números reais são insuficientes para
dar sentido a símbolos como estes:
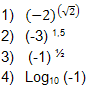
Estes símbolos terão significado no campo dos números complexos.
________________________________________________________________________
Notas Finais
¹Se
você quiser relembrar potenciação e resumir este assunto,
veja os vídeos:
http://www.youtube.com/watch?v=3y6S_36eW8g&NR=1
http://www.youtube.com/watch?v=90xhMs2pELQ
²Se
você quiser relembrar e resumir este assunto, veja os vídeos:
http://www.youtube.com/watch?v=ELy7nXpgYYw&feature=channel
http://www.youtube.com/watch?v=ca18qhF71N8&feature=related
____________________________________________________________________________________