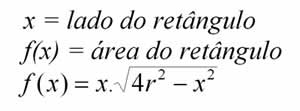Funções definidas a partir de situações geométricas
A
atividade aqui proposta tem como objetivo trabalhar com funções
e geometria, usando o software Régua
e Compasso. A idéia é
construir uma situação geométrica,
usar o dinamismo da figura para estabelecer relações
entre variáveis , pensar qualitativamente
sobre esta relação, construir o gráfico
da função associada as variáveis
na situação geométrica, para então
finalmente determinar a sua lei algébrica e então
responder, através de cálculos, as observações
qualitativas feitas em um primeiro momento.
Sugestões de situações problemas são esboçadas
abaixo. Na primeira situação detalhamos como fazer
uso do Régua e Compasso
para construir a situação geométrica , bem como o gráfico
correspondente.
Situação - problema 1
1. Construa um retângulo R inscrito em um círculo. Inicie a construção com o círculo e a partir de uma corda AB construa o retângulo. Movimente o ponto A e observe a variação da área do retângulo conforme muda o tamanho do lado AB. |
2. Se
x = comprimento de AB
y = área do retângulo R.descreva, em palavras, como é o comportamento da função y = f (x).
Construa o gráfico desta função , sem usar a sua “lei”.
3. Movimente o ponto A e observe o correspondente movimento do ponto no gráfico da função. É possível determinar o retângulo de área máxima?
4. Encontre a lei da função. Usando a lei da função explique como se determina o retângulo de área máxima.
5. Construa o gráfico da função, agora utilizando a sua lei.
6. Quando se muda o tamanho do círculo, o que acontece com o gráfico da função?
Comentário para o professor:
Ao final da atividade o aluno deve ter como produção uma animação da situação geométrica com o correspondente gráfico, acompanhada da expressão da função. Com isto pode responder as perguntas colocadas ao longo da atividade, agora de forma mais precisa.Clique nos ícones
e
, depois no ponto verde, no círculo e por último no ponto vermelho para animar a construção.
Uma possível solução para o problema
Situação - problema 2
Imagine um jogo de futebol. O jogador vai cobrar um pênalti. Qual a distância percorrida pela bola em função do ângulo em que o jogador chutou?
Movimente o goleiro para analisar a situação.
Esta situação pode ser pensada como uma função. Movimente o goleiro para visualizar o gráfico.
À primeira vista, o desenho do gráfico nos faz pensar em parábola. Será?
Uma possível solução para o problema