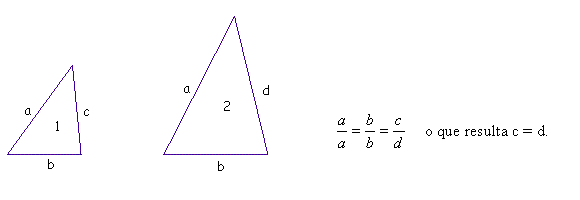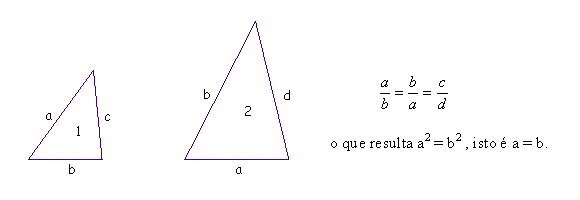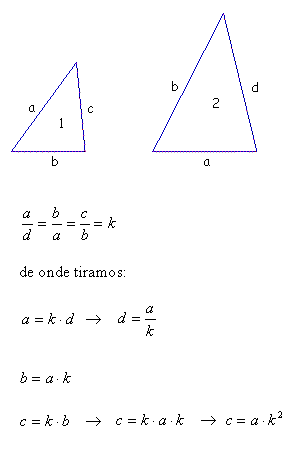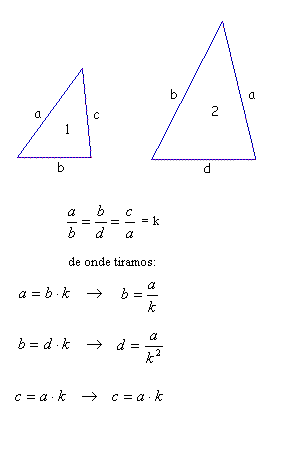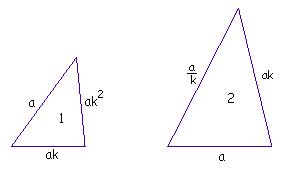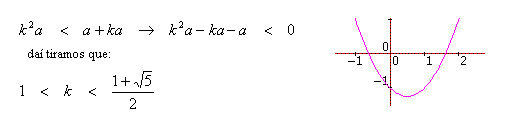
Não podemos deixar de salientar o quanto a ordem em que estes elementos (ângulos e lados) aparecem é importante. Por exemplo no caso LAL, precismos que os triângulos apresentem dois lados e o ângulo entre estes congruentes. Esta ordem é fundamental, senão nada podemos afirmar sobre a congruência dos triângulos.
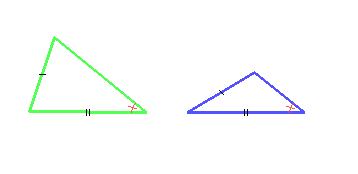
Temos aqui um exemplo de dois triângulos que possuem dois lados e um ângulo congruentes, mas que são visivelmente não-congruentes.
Vamos ver como foi feita esta construção !
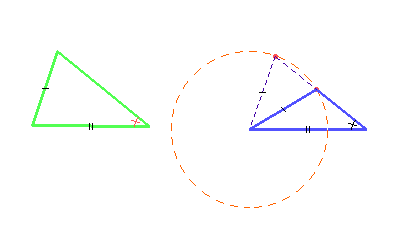
Observe na figura abaixo que o segundo triângulo (o menor) está contido dentro de um triângulo maior (tracejado) que é exatamente igual ao primeiro triângulo. Então, o triângulo menor está contido no triângulo maior!
Observe também qual é o raio da circunferência tracejada? -É o lado do triângulo em congruência nas duas figuras!
Veremos agora, um caso curioso de triângulos que apresentam 5 de seus 6 elementos em congruência, mas que apesar disto não são congruentes.
Em primeiro momento precisamos verificar quais são estes 5 elementos dos triângulos que serão congruentes. Temos duas opções: 3 lados e 2 ângulos em congruência ou 3 ângulos e 2 lados em congruência. A primeira opção deve ser descartada já que sabemos que três lados em congruência é um dos casos que já conhecemos de congruência de triângulos (LLL).
Concluimos então que os nossos triângulos devem ter 3 ângulos e 2 lados em congruência. Então estes triângulos devem ser semelhantes (devem ter lados em proporção) já que existe um caso de semelhança de triângulos que diz:
"Se dois triângulos possuem dois ângulos ordenadamente congruentes, então eles são semelhantes"
Suponhamos então que estes dois triângulos (de ângulos congruentes) tenham lados a, b e c (triângulo 1) e lados a, b e d (triângulo 2). Assim sendo temos quatro possibilidades de pares de lados correspondentes que se mantêm em razão constante nos dois triângulos.

Não podemos deixar de salientar o quanto a ordem em que estes elementos (ângulos e lados) aparecem é importante. Por exemplo no caso LAL, precismos que os triângulos apresentem dois lados e o ângulo entre estes congruentes. Esta ordem é fundamental, senão nada podemos afirmar sobre a congruência dos triângulos.
Temos aqui um exemplo de dois triângulos que possuem dois lados e um ângulo congruentes, mas que são visivelmente não-congruentes.
Vamos ver como foi feita esta construção !

Observe na figura abaixo que o segundo triângulo (o menor) está contido dentro de um triângulo maior (tracejado) que é exatamente igual ao primeiro triângulo. Então, o triângulo menor está contido no triângulo maior!
Observe também qual é o raio da circunferência tracejada? -É o lado do triângulo em congruência nas duas figuras!
Veremos agora, um caso curioso de triângulos que apresentam 5 de seus 6 elementos em congruência, mas que apesar disto não são congruentes.
Em primeiro momento precisamos verificar quais são estes 5 elementos dos triângulos que serão congruentes. Temos duas opções: 3 lados e 2 ângulos em congruência ou 3 ângulos e 2 lados em congruência. A primeira opção deve ser descartada já que sabemos que três lados em congruência é um dos casos que já conhecemos de congruência de triângulos (LLL).
Concluimos então que os nossos triângulos devem ter 3 ângulos e 2 lados em congruência. Então estes triângulos devem ser semelhantes (devem ter lados em proporção) já que existe um caso de semelhança de triângulos que diz:
"Se dois triângulos possuem dois ângulos ordenadamente congruentes, então eles são semelhantes"
Suponhamos então que estes dois triângulos (de ângulos congruentes) tenham lados a, b e c (triângulo 1) e lados a, b e d (triângulo 2). Assim sendo temos quatro possibilidades de pares de lados correspondentes que se mantêm em razão constante nos dois triângulos.