Quando falamos em figuras iguais, intuitivamente nos vem à mente figuras de mesmo tamanho e forma. Isto significa que através de movimentos as figuras se "encaixam" exatamente umas sobre as outras. Observemos que a palavra "iguais" está sendo usada de forma um tanto imprópria, já que o conjunto de pontos que formam cada uma das figuras são diferentes. Tornamos mais precisa nossa linguagem usando a expressão "figuras congruentes". Assim, figuras congruentes são figuras tais que se podem fazer coincidir. Por exemplo, como poderíamos construir réplicas das figuras abaixo? Ou seja, como construir pares de figuras congruentes?

Vamos começar considerando figuras bem simples: - TRIÂNGULOS!! Na Geometria Plana é dito que dois triângulos são congruentes quando os lados e ângulos do primeiro triângulo estão em correspondência com os lados e ângulos do segundo triângulo de tal forma que os lados em correspondência têm a mesma medida, assim como os ângulos. Assim, para determinar a congruência de dois triângulos olhamos para seis elementos em cada triângulo (três lados e três ângulos)e comparamos as medidas. Mas de fato, é suficiente que se conheçam apenas TRÊS destes elementos, numa certa ordem, para termos a congruência assegurada. É isso que nos dizem os critérios, talvez já bem conhecidos, de congruências de triângulos: LAL, ALA, LLL. VAMOS NOS CONVENCER DE QUE ESTES CRITÉRIOS FUNCIONAM QUANDO QUEREMOS DETERMINAR SE DOIS TRIÂNGULOS SÃO CONGRUENTES!! LAL - lado, ângulo, lado - Imagine duas varetas e um ângulo qualquer fixo entre elas. Quantos triângulos podemos construir com este material? Veja Resposta LLL - lado, lado, lado -Imagine três varetas de comprimentos diferentes.Quantos triângulos podemos construir com estas varetas? Dadas três varetas é sempre possível construir um triângulo? Pense nisto! Veja Resposta ALA - ângulo, lado, ângulo -Quantos triângulos seríamos capazes de construir com estes três elementos dados? Veja Resposta

---

É importante lembrarmos que a ordem em que aparecem os elementos é de fundamental importância para que tenhamos, de fato, triângulos congruentes. Podemos ter triângulos com 2 lados e 1 ângulo iguais e a congruência não se verificar. É possível termos também caso em que 5 elementos nos dois triângulos são iguais (3 ângulos e 2 lados) e mesmo assim não termos a congruência entre esses triângulos. Para saber mais sobre estes casos clique aqui. Os critérios nos garantem que conhecendo três de certos elementos do triângulo, numa certa ordem, podemos calcular os demais. E para isto basta usarmos o Teorema de Pitágoras, as Leis dos Senos e Cossenos e o Teorema dos 180 graus. Veja alguns exemplos! Usando material concreto (varetas) nos convencemos de que os critérios acima funcionam. Com isso fica fácil construirmos dois triângulos congruentes. Queremos porém, ir mais adiante: construir figuras congruentes mesmo que não tenham lados ou ângulos. Você pode imaginar algumas maneiras de se fazer isto? Vamos aqui construir tais figuras usando instrumentos especiais.   Antes disso entenda o que são transformações geométricas:

TRANSFORMAÇÕES

Definimos uma transformação geométrica como sendo uma correspondência, um a um, entre pontos de um mesmo plano ou de planos diferentes. Algumas transformações recebem nomes especiais por apresentarem algumas características específicas. Nosso propósito aqui é estudar transformações que quando aplicadas a figuras do plano não alteram as medidas da figura, ou seja, são transformações que relacionam figuras congruentes. São as ditas transformações isométricas. Cada um dos instrumentos que apresentamos anteriormente corresponde a uma certa transformação isométrica: translação ou reflexão ou rotação. Usando as idéias intuitivas que são sugeridas por estes nomes, procure relacionar cada instrumento com a transformação correspondente:

Instrumento 1	Instrumento 2	Instrumento 3
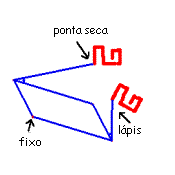
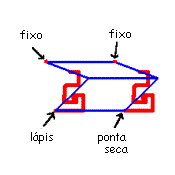
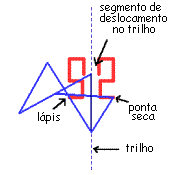
reflexão ?	reflexão ?	reflexão ?
rotação ?	rotação ?	rotação ?
translação ?	translação ?	translação ?