© 2001-2019 Instituto de Matemática e Estatística — UFRGS

MAT 01354   Cálculo e Geometria Analítica IIA

QUÁDRICAS: O Cone Elíptico

O Cone Elíptico Girando em Torno da Origem
Cone Elíptico

A equação-padrão do cone elíptico (ou, mais precisamente, da superfície cônica de duas folhas, já que o termo "cone" costuma ser usado para o sólido que esta superfície limita junto com um, ou dois, planos) é

Equação-Padrão do Cone Elíptico

sendo convencionado que os parâmetros a, b e c são todos positivos. As razões a/c e b/c destes parâmetros dão as inclinações da geratriz deste cone nos planos coordenados verticais, ou seja, das retas concorrentes obtidas no corte deste cone pelos planos coordenados y = 0 e x = 0 de equações, respectivamente,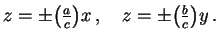

Equação do Corte do Cone Elíptico com os Planos Coordenados Verticais
Observe que o único corte do cone elíptico com o plano x y é dado pela origem, já que substituindo z = 0 na equação-padrão do cone elíptico obtemos
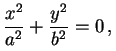
Equação do Corte do Cone Elíptico com o Plano xy
cuja única solução é a origem (x, y) = (0, 0). Em particular, a origem é o único ponto de corte do cone elíptico com os eixos coordenados.

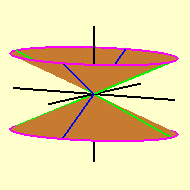
Os Cortes do Cone Elíptico pelos Planos Coordenados Os Cortes do Cone Elíptico pelos Planos Coordenados

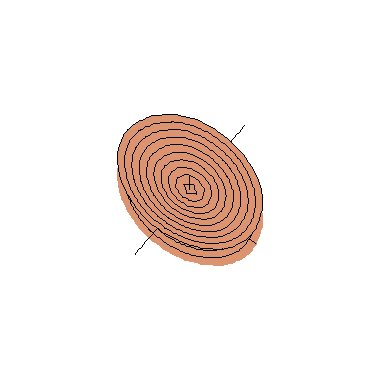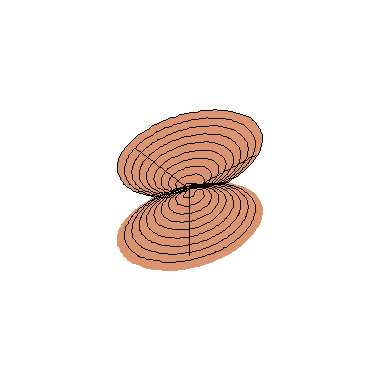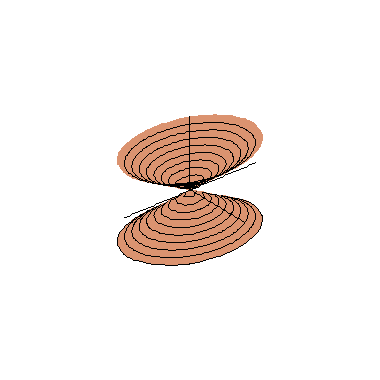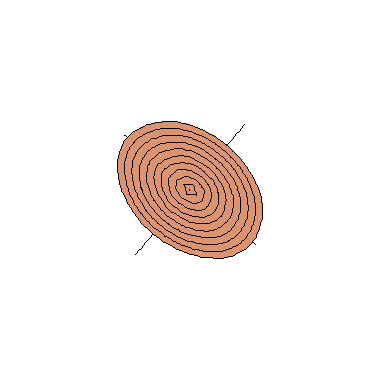
         Os cortes do cone elíptico com os planos coordenados verticais são os pares de retas concorrentes que aparecem nas cores verde e azul nas figuras ao lado; à esquerda temos os dois pares de retas no cone elíptico transparente e à direita aparecem (partes d)estas curvas no mesmo cone elíptico, agora pintado de marrom. Nestas figuras também aparecem em carmim os cortes do cone elíptico por dois planos horizontais z = ± k, que são as elipses de equações Os Cortes do Cone Elíptico no Primeiro Octante

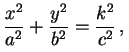
Equação do Corte do Cone Elíptico com Planos Horizontais
para qualquer constante k não-nula. Na figura à direita, vemos as partes de todas estas curvas que aparecem no primeiro octante.

         Convém observar que o que é exibido nestas figuras é só uma parte do cone elíptico, que se estende indefinidamente em todos os seis sentidos do espaço tridimensional; no entanto, como ocorre com os hiperbolóides de uma e de duas folhas (dos quais o cone é um caso limite, como pode ser observado aqui), basta entender o comportamento do cone na vizinhança da origem, pois o resto é bastante previsível.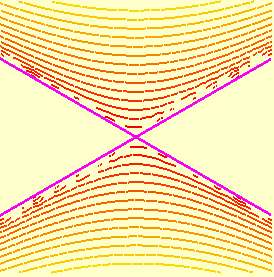

Curvas dos Cortes por Planos Verticais Paralelos aos Planos Coordenados

         Os cortes do cone elíptico com qualquer plano vertical paralelo a um dos planos coordenados x z ou y z, mas que não contém a origem, sempre produz uma hipérbole, de equação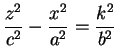

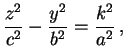
As Equações dos Cortes Verticais do Cone Elíptico
ou
As Equações dos Cortes Verticais do Cone Elíptico
tomando, respectivamente, y = ± k ou x = ± k constante. Na figura, as retas concorrentes limites em carmim são obtidas pelo corte dos planos coordenados verticais.

Curvas de Nível do Cone Elíptico

         O cone elíptico nunca é o gráfico de uma função real de duas variáveis reais; no entanto, como quase sempre ocorrem dois cortes por retas verticais, podemos separá-lo em dois gráficos, dados pelas duas funções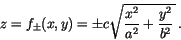

As Duas Funções Cujos Gráficos Formam o Cone Elíptico
As curvas de nível de cada uma destas funções aparecem ao lado: são as elipses vistas acima, dadas pelos cortes por planos horizontais; o corte pelo plano coordenado horizontal é o ponto na origem que aparece em carmim.

         Concluímos esta visualização do cone elíptico observando que tomando a = b na equação-padrão, obtemos um cone circular, que sempre é uma superfície de revolução. Esta superfície é usualmente utilizada para definir as curvas cônicas geometricamente: o corte de qualquer plano com o cone circular é sempre uma cônica (o que pode ser observado, cinematicamente, aqui). É interessante observar, entretanto, que o mesmo ocorre tomando um cone elíptico qualquer.


hiperbolóide de duas folhas quádricas hiperbolóide de uma folha