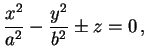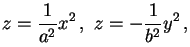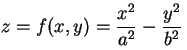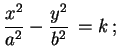© 2001-2019 Instituto de Matemática e Estatística — UFRGS

MAT 01354   Cálculo e Geometria Analítica IIA

QUÁDRICAS: O Parabolóide Hiperbólico

A equação-padrão do parabolóide hiperbólico é

Equação-Padrão do Parabolóide Hiperbólico

sendo convencionado que a > 0 e b > 0. (Nesta página, tomamos o sinal - desta equação.)

Parabolóide Hiperbólico

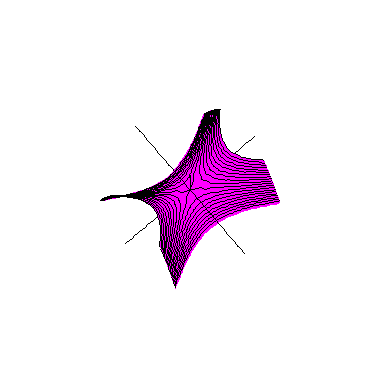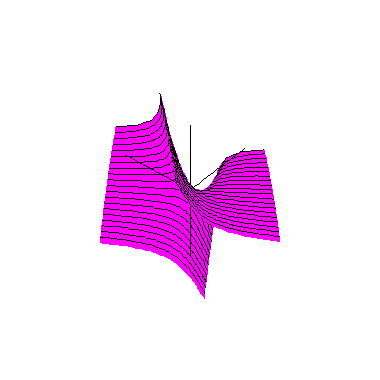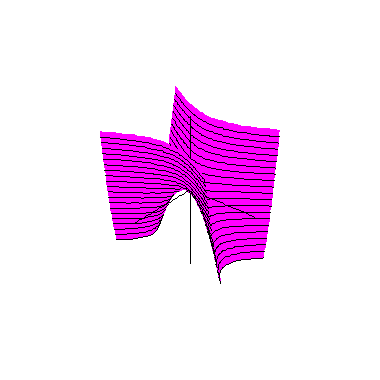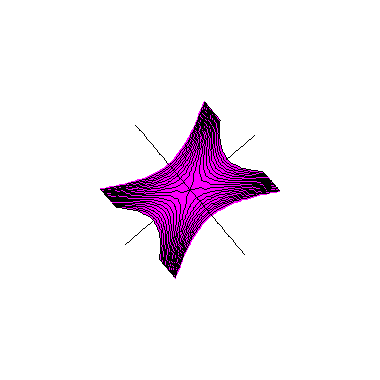
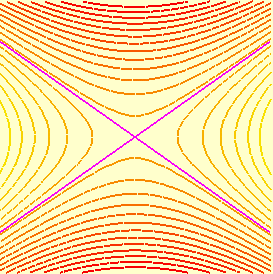
         Não há cortes do parabolóide hiperbólico com os eixos coordenados, exceto pela origem: tomando duas variáveis nulas na equação do parabolóide hiperbólico, obtemos sempre a origem (0, 0, 0), que é o ponto de sela do parabolóide. Já o corte do parabolóide hiperbólico com o plano coordenado x y é o par de retas concorrentes dadas por

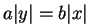
O Corte do Parabolóide Hiperbólico no Primeiro Octante Equação do Corte pelo Plano Coordenado Horizontal

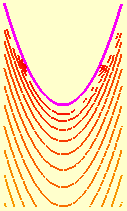
e o corte do parabolóide hiperbólico com os planos coordenados verticais y = 0 e x = 0, são as parábolas dadas por

Equação das Parábolas nos Cortes pelo Plano Coordenado Vertical

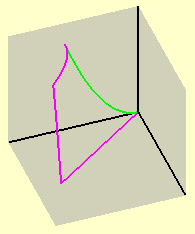
sendo que só (metade d)a primeira aparece de verde no primeiro octante, ao lado; neste octante também vemos uma semi-reta horizontal na cor carmim.

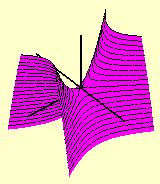
As duas parábolas dadas pelos cortes com os planos coordenados verticais aparecem nas figuras abaixo: à esquerda temos as duas parábolas no parabolóide hiperbólico transparente e à direita aparecem (partes d)estas curvas no mesmo parabolóide hiperbólico, agora pintado de marrom.

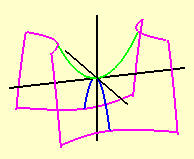
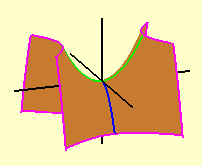
Os Cortes do Parabolóide Hiperbólico pelos Planos Coordenados Os Cortes do Parabolóide Hiperbólico pelos Planos Coordenados

Nas figuras acima também aparecem em carmim os cortes do parabolóide hiperbólico por quatro planos dados por x = ± constante e z = ± constante; como veremos a seguir, nos dois planos verticais as curvas são (partes de) parábolas e nos dois planos horizontais as curvas são (partes de) hipérboles.

         Convém observar que o que é exibido nestas figuras é só uma parte do parabolóide hiperbólico, que se estende indefinidamente em todos os seis sentidos do espaço tridimensional; no entanto, basta entender o comportamento do parabolóide na vizinhança do ponto de sela, pois o resto tem um comportamento semelhante. Também observamos que o parabolóide hiperbólico nunca é uma superfície de revolução.

Curvas de Nível do Parabolóide Hiperbólico
Cortes Horizontais

 

Curvas dos Cortes por Planos Verticais Curvas dos Cortes por Planos Verticais
Cortes Verticais

         O parabolóide hiperbólico evidentemente é o gráfico da função real

A Função cujo Gráfico é Parabolóide Hiperbólico

de duas variáveis reais obtida da equação-padrão. As curvas de nível desta função são as hipérboles dadas pelos cortes horizontais, de equação

Equação do Corte pelos Planos Horizontais

à esquerda, aparece o mapa de contornos desta função. (Uma versão cinemática deste mapa de contornos pode ser conferida aqui.)

Por outro lado, os cortes por planos verticais paralelos aos eixos coordenados, sempre resultam em parábolas, como indicamos nas duas figuras acima à direita, nas quais as parábolas limites em carmim são obtidas pelos planos coordenados verticais pela origem.

         Concluímos esta visualização do parabolóide hiperbólico deixando-o girar livremente em torno do ponto de sela:

Parabolóide Hiperbólico Girando em Torno do Ponto de Sela


parabolóide elíptico de volta às quádricas