Equação da elipse com centro na origem do sistema de coordenadas

Imagine dois pontos fixos no plano. Uma elipse é o conjunto de todos os pontos do plano tal que a soma das distâncias aos dois pontos fixos dados (chamados de focos) é igual a uma constante positiva determinada.

O ponto médio do segmento que une os focos é chamado de centro. Observe:

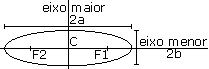
No triângulo retângulo destacado na figura abaixo podemos observar as seguintes relações:

Como a soma das distâncias dos pontos que compõe a elipse aos focos é constante podemos afirmar que:

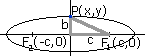
A soma das distâncias de qualquer ponto da elipse aos focos é igual a uma constante positiva 2a, logo:

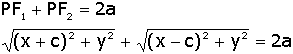
Passando o segundo membro do lado esquerdo da igualdade para o outro lado e elevando ao quadrado temos:

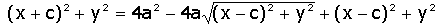
Simplificando obtém-se:

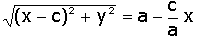
Elevando a igualdade novamente ao quadrado e efetuando algumas simplificações obtemos:

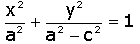
Substituindo 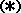na equação acima obtemos a equação geral da elipse:



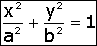
Esta é a equação para uma elipse que tem como centro o ponto (0,0).

Equação da elipse cujo centro não está na origem do sistema de coordenadas

Caso queiramos saber qual é a equação de uma elipse cujo centro não está na origem do sistema de coordenadas xy podemos criar um novo sistema x'y' para determinarmos qual é a equação desta elipse:

A equação da elipse no sistema x'y' é:

Para podermos escrever a equação desta elipse no sistema xy basta sabermos como escrevemos x' e y' em relação ao sistema xy.

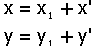, logo

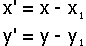
Logo, a equação da elipse no sistema xy é :

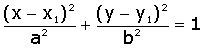
Sendo 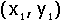o centro da elipse no sistema xy.

Desigualdades
A relação de desigualdade 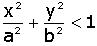representa todos os pontos P = (x , y) que estão no interior da região delimitada pela elipse de centro O = (0,0) e eixos de comprimento 2a e 2b.
Já a relação de desigualdade 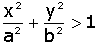representa todos os pontos P = (x , y) que estão no exterior da região delimitada pela elipse de centro O = (0,0) e eixos de comprimento 2a e 2b.

Observe a animação:
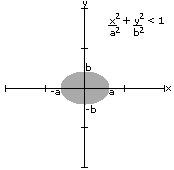