Equação da parábola

Dados um ponto F e uma reta d que não contenha F, o conjunto de pontos P = (x , y) que distam igual valor de F e de A é o que denomina-se uma parábola de foco F e diretriz d.

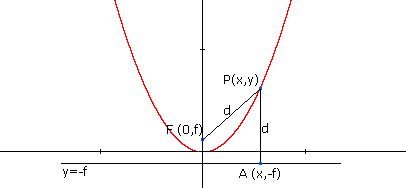
Para determinar a equação da parábola iniciamos escolhendo um sistema de coordenadas conveniente de forma tal que: o foco F tem coordenadas (0,f) ; a diretriz tem equação y = - f .

Sendo P = (x , y) um ponto qualquer da parábola, podemos escrever :

                       

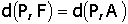
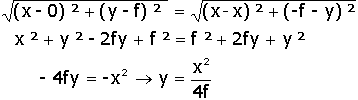
Como f é uma constante qualquer, podemos fazer 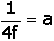. Daí temos:

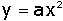
Análise do coeficiente a

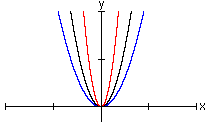
Na figura acima, temos, em preto a parábola y = x ² e em vermelho a parábola de equação y = ax ², com a > 1 .
Temos também, em azul, a parábola y = ax ², com 0 < a < 1 .

Com esta análise de gráficos, vemos que é o valor do coeficiente a que determina o quão fechada ou aberta é a parábola, e também se é uma parábola voltada para cima ou para baixo. Pois se a<0 a equação y = ax ² produz um gráfico cujos valores de y são sempre negativos.

Deslocamento vertical

O efeito que uma parábola de equação y = a. x ² sofre ao adicionarmos uma constante b a sua expressão, deixando-a da forma y = a.x ² + b, chama-se deslocamento vertical.
Analisando o gráfico da figura abaixo, podemos ver que a cada valor y da função y = a x², estamos adicionando b unidades. Não podemos esquecer que b assume qualquer valor, positivo ou negativo. Na figura abaixo temos o caso em que b>0 , quando a parábola "sobe b unidades" em relação ao gráfico de y = a. x ²; no caso b <0 a parábola "desce -b unidades" .

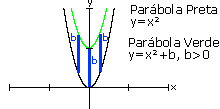
Deslocamento horizontal

O efeito que uma parábola de equação y = a. x ² sofre ao adicionarmos uma constante b a x , deixando a expressão da forma y = a.(x+b) ², chama-se deslocamento horizontal.

Na equação y = ax² a coordenada x do vértice da parábola é 0. Sabemos disso, pois bem no vértice y vale zero então temos:

ax²=0, logo x=0

Já na equação y = a.(x+b) ²,quando y = 0, a(x+b)²=0, logo x = -b.

Portanto em equações do tipo y = a.(x+b) ², a coordenada x do vértice será sempre -b.

Observe que a parábola acima está deslocada b unidades para a direita. As novas coordenadas dos pontos que compõe a parábola são:
x = x'+b
y = y'     logo,

x = x'-b

Exemplo: Vamos localizar a parábola y=-(x-4)²-2

Para localizar esta parábola seguimos os seguintes passos:
1) Localizamos a parábola y=x²
2) Como estão sendo diminuídas quatro unidades de x, transladamos a parábola na horizontal 4 unidades para a direita.
3) Refletimos a parábola em relação ao eixo x, por causa do sinal de - antes de (x-4)²
4) Transladamos verticalmente a parábola 2 unidades para baixo.

Clique na figura abaixo para ver um exemplo animado:



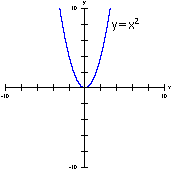
Desigualdades

A relação de desigualdade y > a x² + b é satisfeita pelos pontos P = (x, y) que estão na região assinalada na figura 17.
A relação de desigualdade y < a x² + b é satisfeita pelos pontos P = (x, y) que estão na região assinalada na figura 18.

Clique na figura abaixo para ver um exemplo animado:
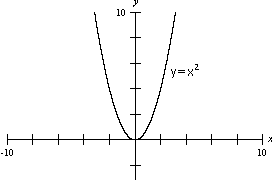