Equação da reta que passa pela origem do sistema de coordenadas:

Observe as retas abaixo, que estão desenhadas em um sistema de eixos cartesianos:
      

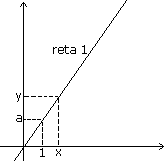
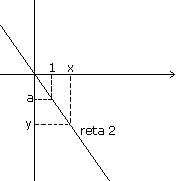
Os triângulos retângulos de catetos medindo, respectivamente 1 e x, possuem os três ângulos congruentes, logo são semelhantes. Podemos, a partir desta verificação, estabelecer as seguintes relações:

Na figura que contém a reta 1 vemos que a > 0 :

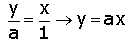
Na figura que contém a reta 2, a < 0:

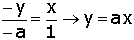
Logo concluímos que a equação da reta que passa pela origem do plano cartesiano é y = a x .

Análise do coeficiente a

a=1
Neste caso temos a reta y=x. Ou seja , a reta formada pelos pontos (x,x).

0<a<1
Neste caso temos uma reta com declividade menor que a reta y=x, pois se 0<a<1, ax será sempre um número menor que x, a não ser para x<0.

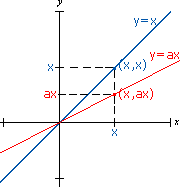
a>1
Neste caso temos uma reta com declividade maior que a reta y=x, Pois se a>1 ax será sempre um número maior que x, a não ser para x<0.

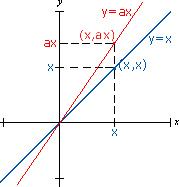
Observe que o sinal do coeficiente nos informa se a reta é crescente ou decrescente. Exemplos:

      

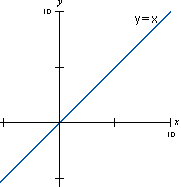
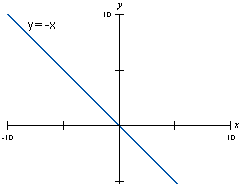
Equação da reta que não passa pela origem do sistema de coordenadas:

Vamos agora determinar a equação de uma reta que não passa pela origem do sistema de coordenadas, efetuando, como exemplo algumas mudanças na equação da reta y = x.

Os pontos da reta y=x são da forma (x,x). Se somarmos na coordenada y de cada ponto um número b (b>0) a reta será transladada verticalmente para cima, pois os pontos serão da forma (x, x+b), com b>0. Observe abaixo:

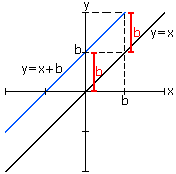
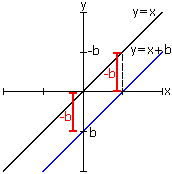
Se b<0 então a reta será transladada verticalmente para baixo. Observe:

Como foi somado b à coordenada y de cada ponto, a equação das retas acima é :



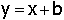
Clique na figura abaixo e observe um exemplo animado:



Na figura acima vemos alguns quadros do movimento de translação vertical da reta y=x

Exemplo : Localizando a reta y= -2x+4

Para localizar esta reta podemos seguir alguns passos que nos auxiliarão:
1) Localizo a reta y=2x
2) A reta y=-2x é simétrica à reta anterior em relação ao eixo y.
3) Translado a reta y=-2x quatro unidades para cima.

Clique na figura abaixo e observe a animação:

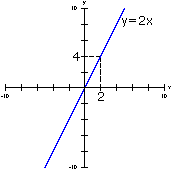
Desigualdades

Todos os pontos P = (x , y) , do plano, que se encontram acima da reta de equação y = a x + b têm as coordenadas satisfazendo a desigualdade

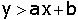
e consequentemente, os pontos P= (x , y) que estão abaixo da reta satisfazem a relação

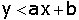
Clique na figura abaixo e veja um exemplo animado:
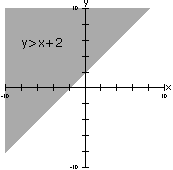