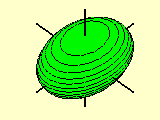
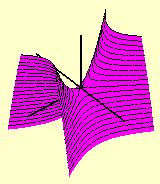
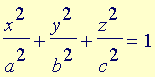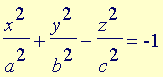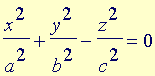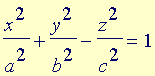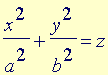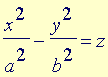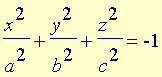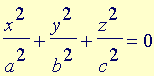Analogamente ao que é feito com as equações do segundo grau nas duas variáveis x e y para classificar as curvas cônicas do plano, também neste caso de três variáveis x, y e z efetuamos uma translação e/ou uma rotação para identificar a equação equivalente em formato padrão. A translação consiste em completar os quadrados, enquanto a rotação, que elimina o(s) termo(s) envolvendo duas variáveis, é bastante mais sutil: este tipo de conta pode ser acompanhada nas disciplinas de Álgebra Linear e não será feita.
O nosso objetivo aqui é meramente apresentar a classificação das quádricas em termos de invariantes. Para isto, convém reescrever a equação geral do segundo grau nas três variáveis x, y e z ordenando os coeficientes, como segue:
a11 x2 + a22 y2 + a33 z2 + 2a12 xy + 2a13 xz + 2a23 yz
+ 2a1 x + 2a2 y + 2a3 z + a0 = 0 .
A forma quadrática associada a esta equação é dada por
a11 x2 + a22 y2 + a33 z2 + 2a12 xy + 2a13 xz + 2a23 yz ,
cuja equação característica é
|
em formato de determinante.
Observe que a equação característica é uma equação de terceiro grau em r . As três raízes r1, r2 e r3 desta equação determinam os invariantes
| J = r1r2 + r1r3 + r2r3
|
||||||||||||||||||||||
|
S = r1 +
r2 + r3 = a11 + a22 + a33 |
d = r1r2r3
| |||||||||||||||||||||
da forma quadrática; além disto, usamos o determinante
|
Com estes quatro invariantes (os números J, S, d e D) podemos classificar todas as seis quádricas não-degeneradas, como segue: